前言

黑体是一个理想化的物体，它能够吸收外来的全部电磁辐射，并且不会有任何的反射和透射。随着温度的上升，黑体所辐射出来的电磁波被称为黑体辐射。实际中的物体对外来的电磁辐射并不能完全吸收，因此它们也被称为“灰体”。“灰体”的热辐射光谱可以通过改变其几何形状或材料来改变。修改或定制物体热辐射曲线的能力在应用物理学和工程学的许多领域都非常重要。人们注意到，在亚波长尺度上对由金属和介电材料组成的器件进行周期性设计可以改变该器件的热辐射性质。本案例根据Chan^[1] 等人的工作，研究了一个由金属钨和折射率为$\sqrt{5}$的介电材料组成的器件周期性排列得到的光子晶体的热辐射现象。

仿真设置

本案例使用的光子晶体由放置在金属钨平板上的具有周期性孔阵列的介质材料组成，下图为该晶体一个单元的结构示意图，其中$a$为光子晶体的晶格常数。由于结构和平面波光源的对称性，我们在$X$方向上使用Anti-Symmetric反对称边界条件；在$Y$方向上使用Symmetric对称边界条件。使用对称和反对称边界条件可以将仿真区域缩小至 1/4，从而减少仿真使用的内存和时间。

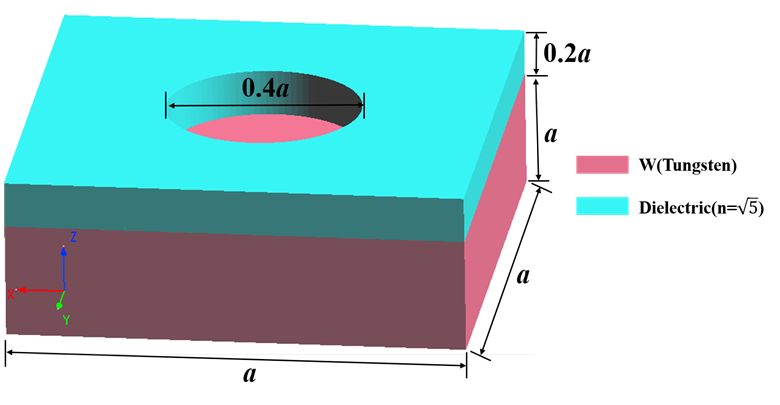
材料设置

本案例中，金属钨的介电常数会影响到器件的性能，故在模拟仿真之前，需要查看其在仿真波段内拟合的模型是否满足仿真需求；如果不满足，请调整拟合误差和多项式最大系数，重新拟合。下图展示了本案例中自动拟合的符合误差要求的结果。

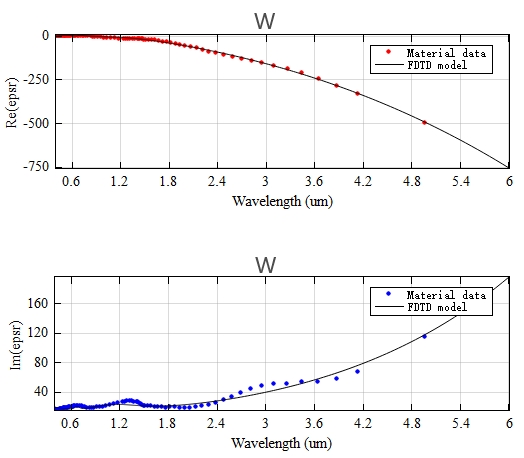
仿真结果

通过结构顶部和底部的Frequency-Domain Field and Power(FDFP)监视器中存储的 T 数据，可以绘制出器件的反射率、透射率以及吸收率（即发射率），下图为光子晶体晶格常数$a$分别为$2\mu m$和$3.23 \mu m$时，发射率随波长的分布。

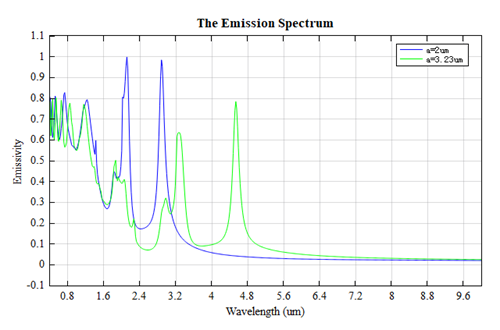
将发射率乘以黑体辐射率即可得到热辐射光谱，他们与黑体辐射光谱一起显示在下图中，与参考文献中的Figure5(b) 一致。本案例中热辐射计算的详细信息可以在附件工程中的thermal_emission_power分析组中找到，关于热辐射的相关信息见附录。

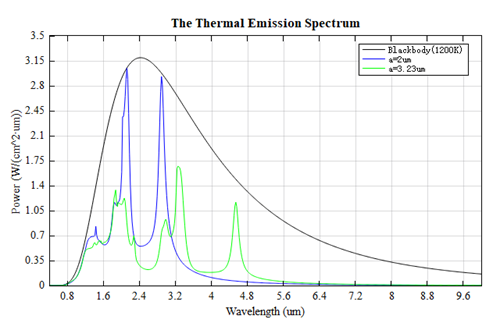
附录

黑体辐射定律

黑体辐射定律（也称为普朗克黑体辐射定律，普朗克定律）揭示了黑体的光谱辐射出射度$E_{\lambda}$与波长$\lambda$和温度$T$的关系。根据量子力学理论得到的普朗克定律有如下的数学表达式：

$E_{\lambda}=\frac{c_1\lambda^{-5}}{e^{c_2/\lambda T}-1}$

其中$T$为绝对温度（单位$K$），$c_1$为第一辐射常量，$c_2$为第二辐射常量，其中 $c_1= 3.742 \times 10^{-16} (W·m^2)$，$c_2= 1.4388 \times 10^{-2} （m·K）$。后来普朗克提出了能量非连续化的假设（在有限个特征频率的谐振子构成的系统），系统的总能量为最小能量单位的整数倍分布，为$hν$，$h$是普朗克常数（$h \approx 6.626 \times 10^{-34}J·s$），则可得到非连续化的普朗克辐射定律:

$E_{\lambda}=\frac{2 \pi hc^2\lambda^{-5}}{e^{hc/k_B\lambda T}-1}$

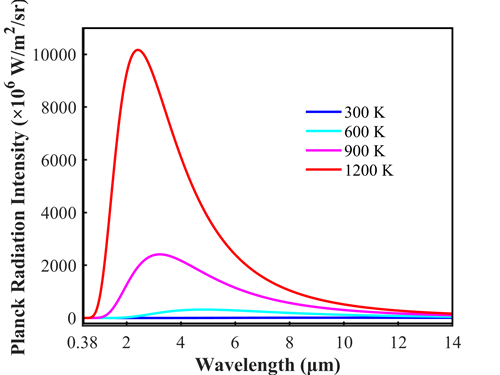
其中$k_B$为玻尔兹曼常数（$k_B\approx 1.381×10^{-23}J·K^{-1}$）。不同温度下黑体的热辐射光谱如下图所示。由图可知，黑体的热辐射和温度有关。温度升高后，辐射强度增加，同时辐射峰蓝移。

参考文献

---

1. Chan D, Soljaci M, Joannopoulos J D. Thermal emission and design in 2D-periodic metallic photonic crystal slabs[J]. Optics Express, 2006, 14(19):8785-96. ↩︎