产品
求解器
学习中心
应用案例
知识库
支持
许可协议
发行说明
最新进展
English
中文
客户下载
应用案例
知识库
联系电话
+86-13776637985
邮箱
info@simworks.net


SimWorks FDFD 是研究人员和工程技术人员分析谐振腔的频谱、金属天线等问题的有力工具。下面,我们会简要介绍FDFD求解器的基本原理和主要特色。
频域有限差分(FDFD)求解器通过求解频域麦克斯韦方程组来计算在目标频率下的电磁场空间分布。FDFD的基本原理如下。
频域麦克斯韦方程组
对于无源材料,麦克斯韦旋度方程具有以下形式:
FDFD网格
FDFD 中的电磁场基于Yee cell网格在空间中交错分布,电场分布在FDFD网格棱线中心,磁场分布在FDFD网格面中心。
FDFD中的材料是基于Yee cell网格进行离散,FDFD网格中的材料检测点和结构形状进行点形逻辑判断,得到符合FDFD网格分布的材料(结构对应的电磁材料)离散分布。
有限差分算法
根据频域麦克斯韦方程,在Yee cell网格上进行差分离散,对于Y轴向磁场分量有:
在空间内沿坐标轴线性展开,可将以上方程转换为如下形式:
同理可知:
其中,、、 和 、、 是包含整个网格中所有电场和磁场分量的列向量;、 和 、 是计算电磁场分量在网格上的空间差分所使用的带状矩阵;和为包含整个网格沿其中心对角线的相对磁导率和介电常数张量分量的对角矩阵。
根据上述方程,将恒定频率下的麦克斯韦方程组转换为矩阵形式:。
矩阵为物理空间中的波动矩阵,列向量为需要求解的电磁场分量,列向量为源。
_20240116095016A033.png)
3D CAD界面和丰富的零件库

网格技术
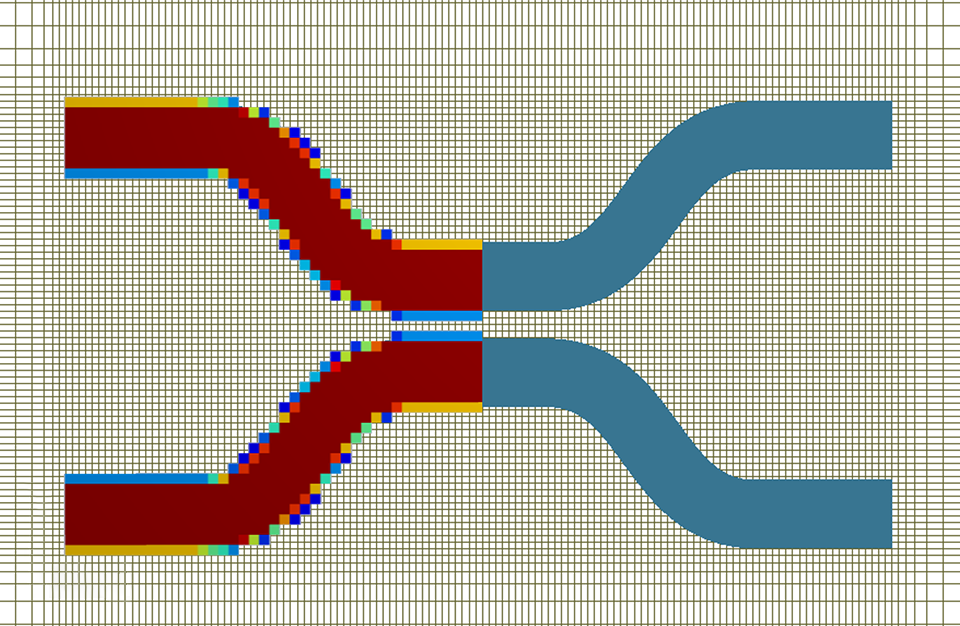
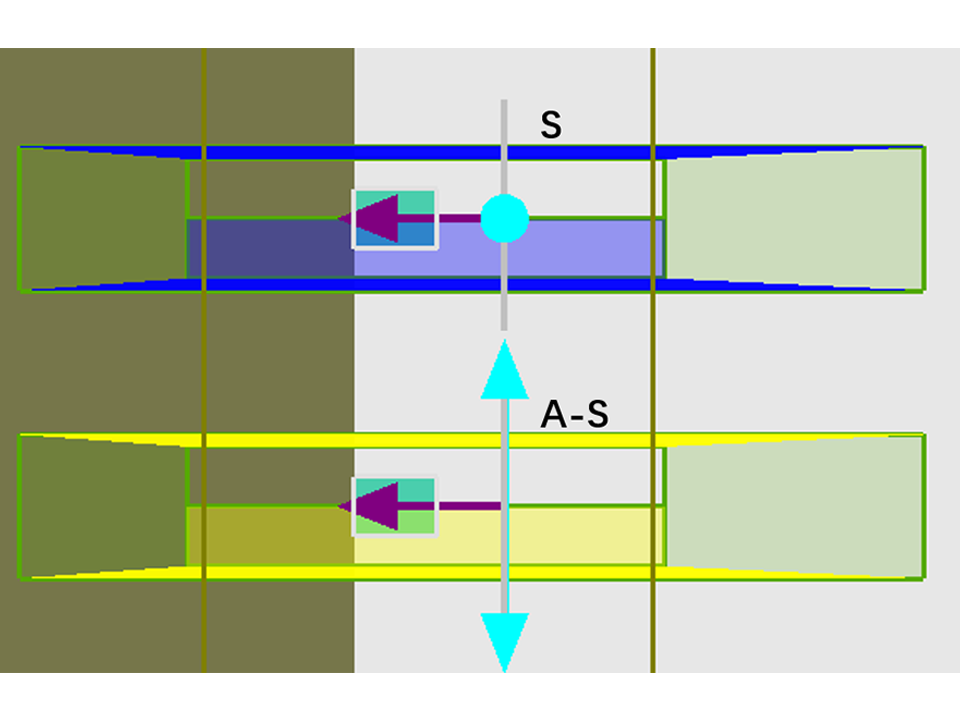
边界条件
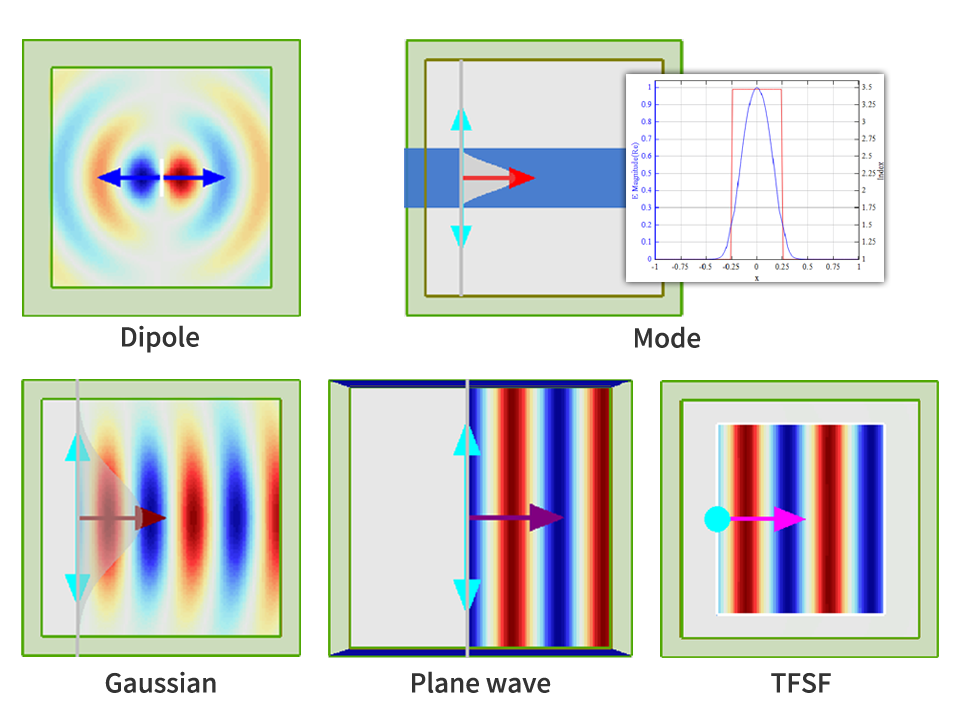
多种光源
材料属性

后处理分析

扫描优化
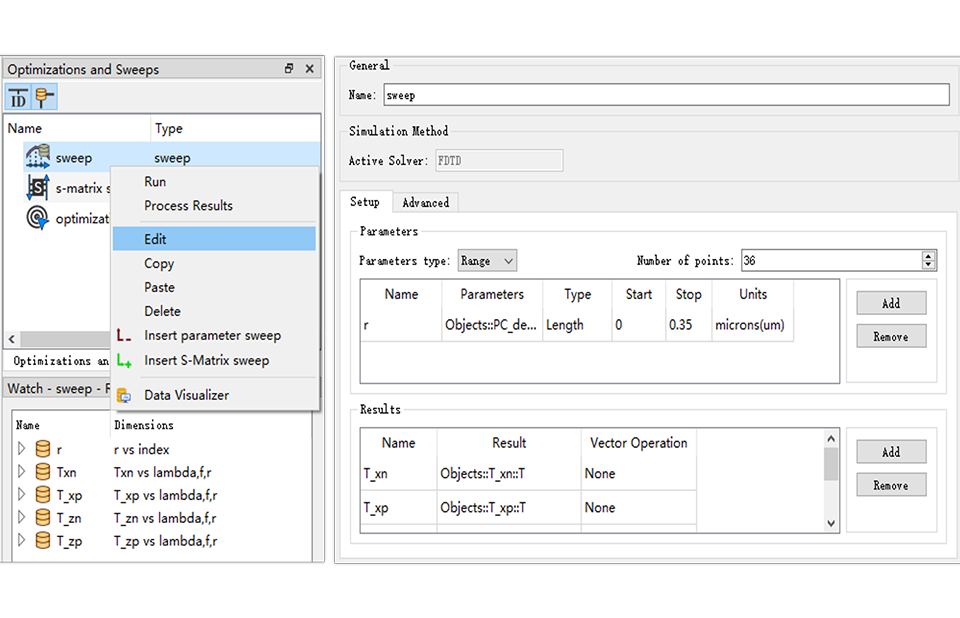
脚本控制
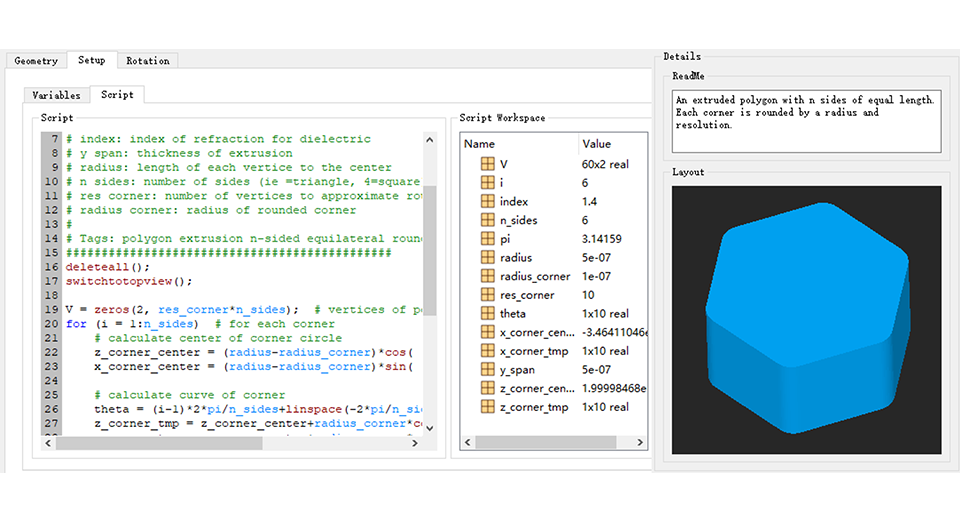
强大的算力
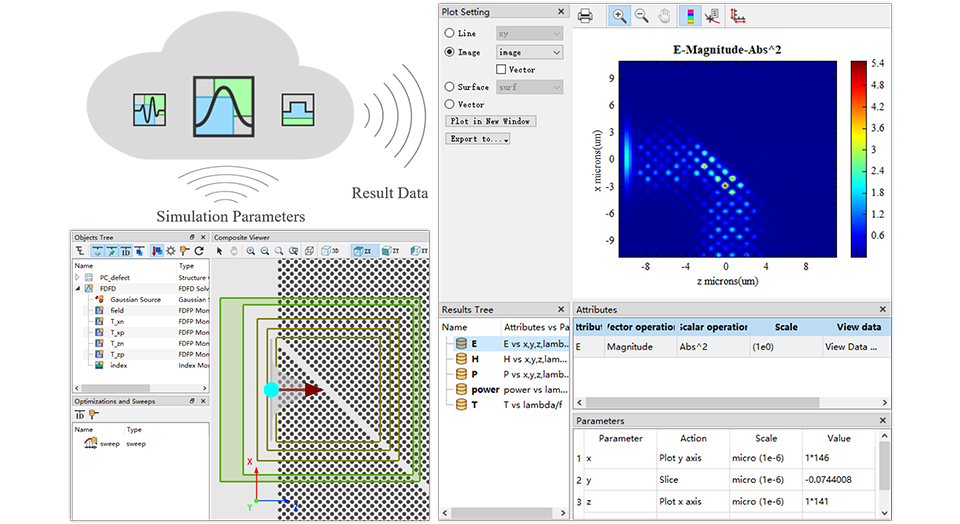
[1] Rumpf, Raymond C et al. “Rigorous electromagnetic analysis of volumetrically complex media using the slice absorption method.” Journal of the Optical Society of America. A, Optics, image science, and vision vol. 24,10 (2007): 3123-34.