产品
求解器
学习中心
应用案例
知识库
支持
许可协议
发行说明
最新进展
English
中文
客户下载
应用案例
知识库
联系电话
+86-13776637985
邮箱
info@simworks.net


SimWorks FDTD 是研究人员和工程技术人员处理各种微纳光电子问题的有力工具。下面,我们会简要介绍求解器的物理原理、求解器的主要特色和求解器的仿真流程。
时域有限差分FDTD是从时域麦克斯韦旋度方程出发,在一定体积内和一段时间上对连续电磁场的数据抽样,它直观地再现了在离散数值时空中电磁现象的物理过程。因此,FDTD是对电磁问题的最本质、最完备的数值模拟,具有广泛的适用性。FDTD求解的是麦克斯韦方程组的时域解,借助傅里叶变换,通过一次仿真即可得到器件在宽频中的频域响应。FDTD的基本原理如下:
对于非磁性材料,麦克斯韦旋度方程可以化为:
根据上述方程, 在Yee cell网格上进行FDTD差分离散:
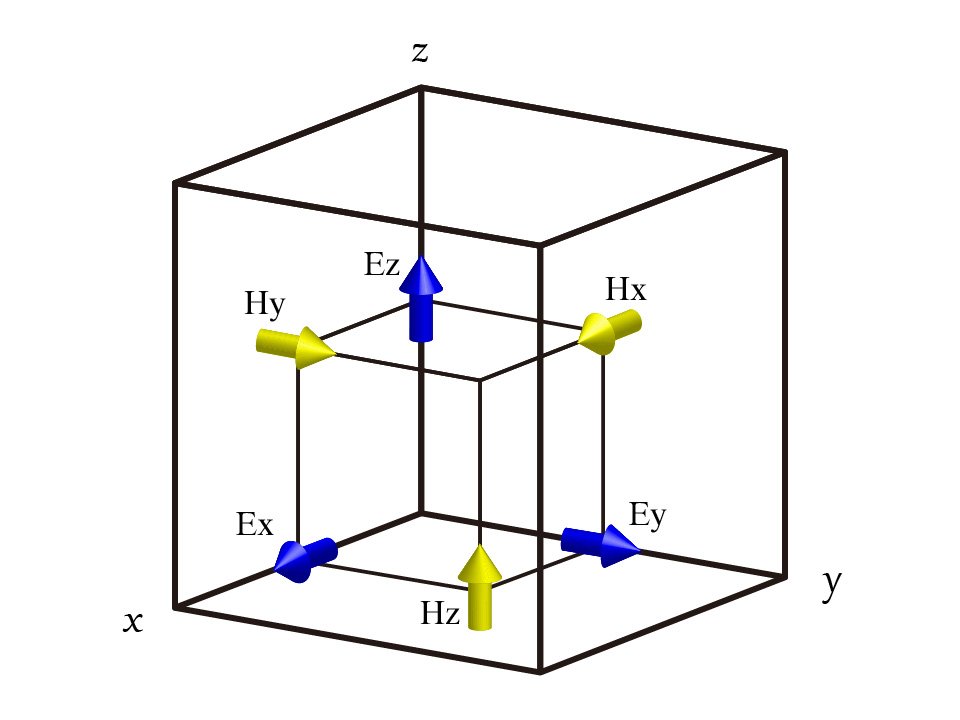
FDTD 中的电磁场基于Yee cell网格在空间中交错分布 (见下图左)。
电场分布在网格棱线中心,磁场分布在网格面中心。每一个电场分量和与它相邻的并且垂直于该电场分量的4个磁场分量,满足麦克斯韦旋度方程(磁场同理)。
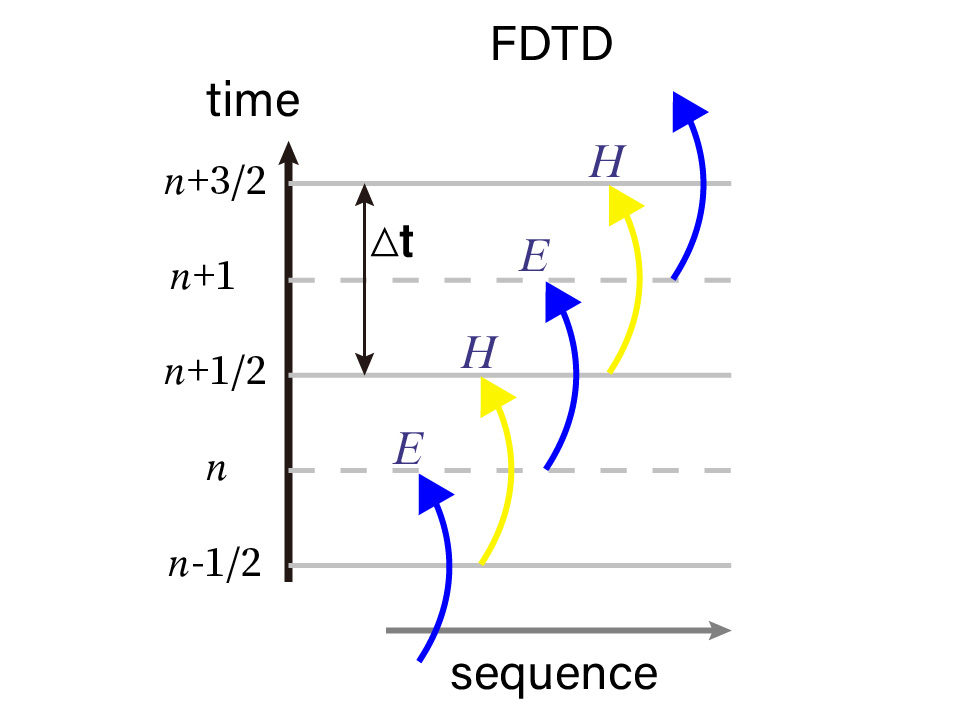
FDTD 中离散化的电磁场在时间上是交错迭代,采用蛙跳法逐步递推求解(见下图中)。
FDTD中 的材料是基于Yee cell网格进行离散 (见右下图)。
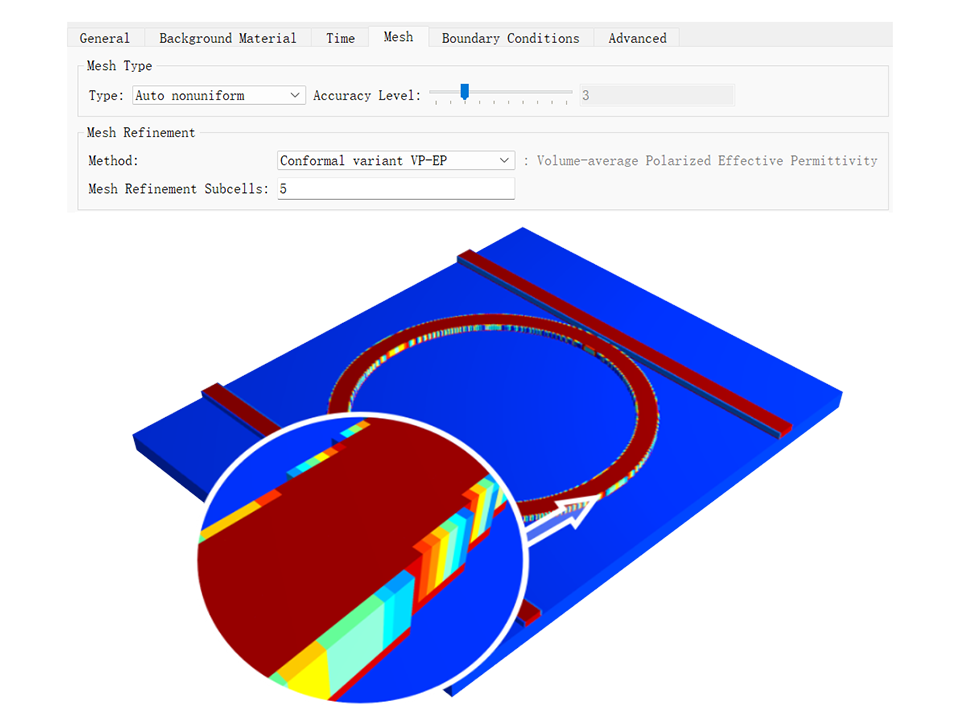
越细的网格能够更好的再现结构,但是会导致内存和仿真时间大大增加。由于网格的选取会严重影响器件的仿真速度和精度,我们为用户提供了自动非均匀网格和各种共性网格等高级选项,具体请见mesh。
- 根据空间网格设置,生成平行于直角坐标系的
FDTD网格(通常称为mesh);FDTD网格中的材料检测点和结构形状进行点形逻辑判断,得到符合FDTD网格分布的材料(结构对应的电磁材料)离散分布。
因此,数值化后的电磁场三维递推方程如下:
三维的其它方向与上面公式类似,详见参考[1,2]。

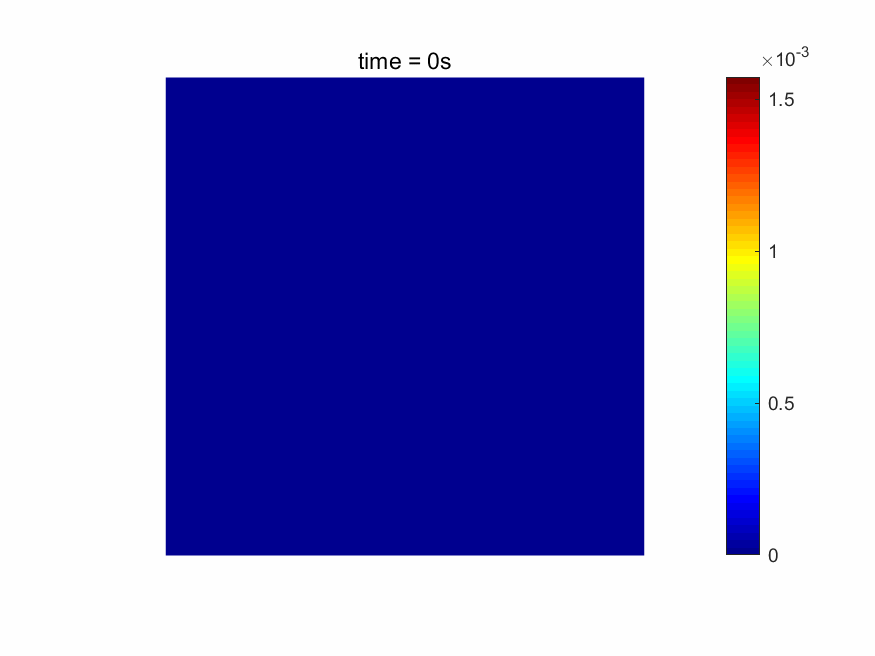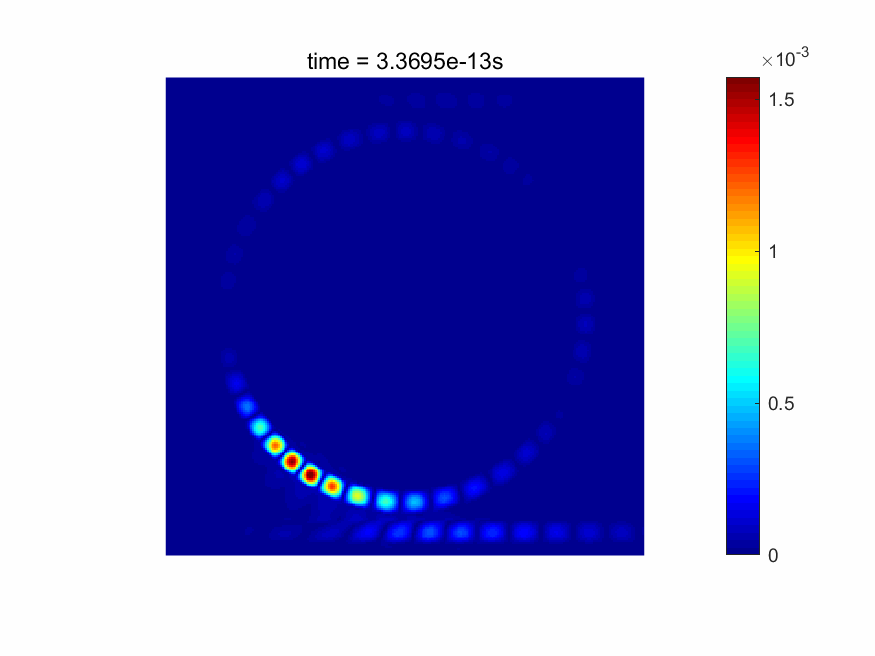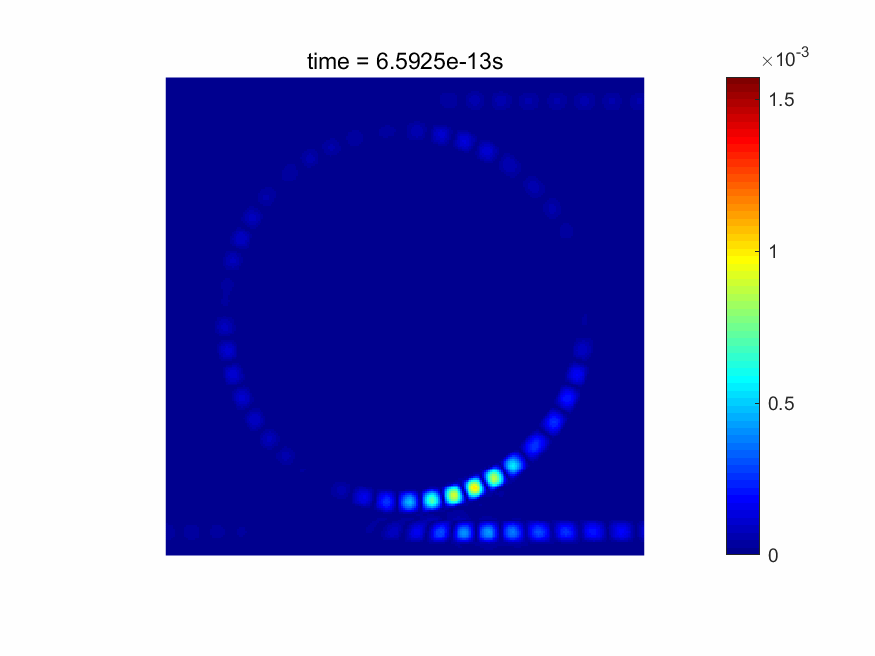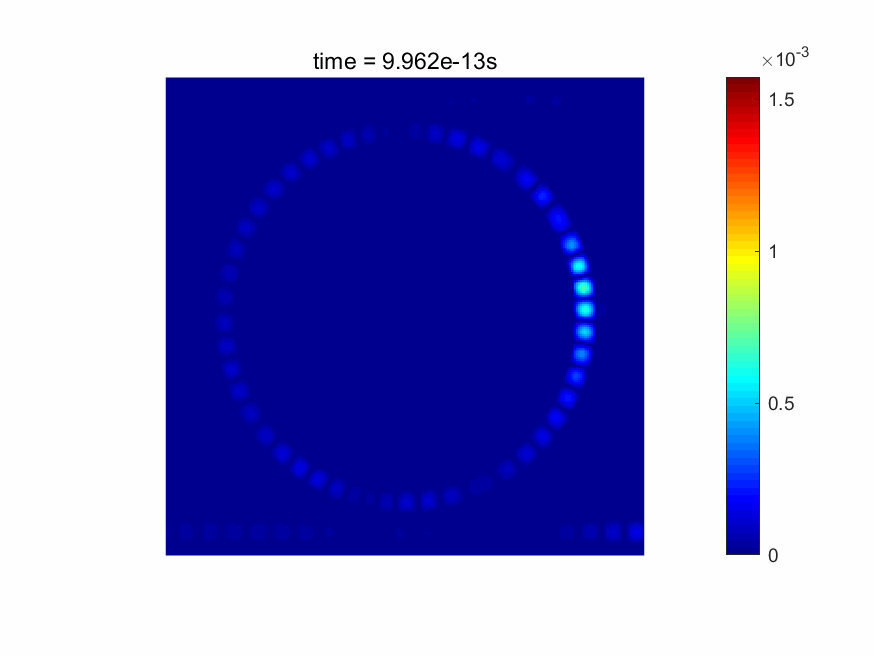
本软件能够实时显示电磁场的时域场图。FDTD仿真后,各个网格点的材料数据、电场/磁场、功率、透过率/反射率等信息也可以直接得到(请见下图)。
_20240919113530A039.png)
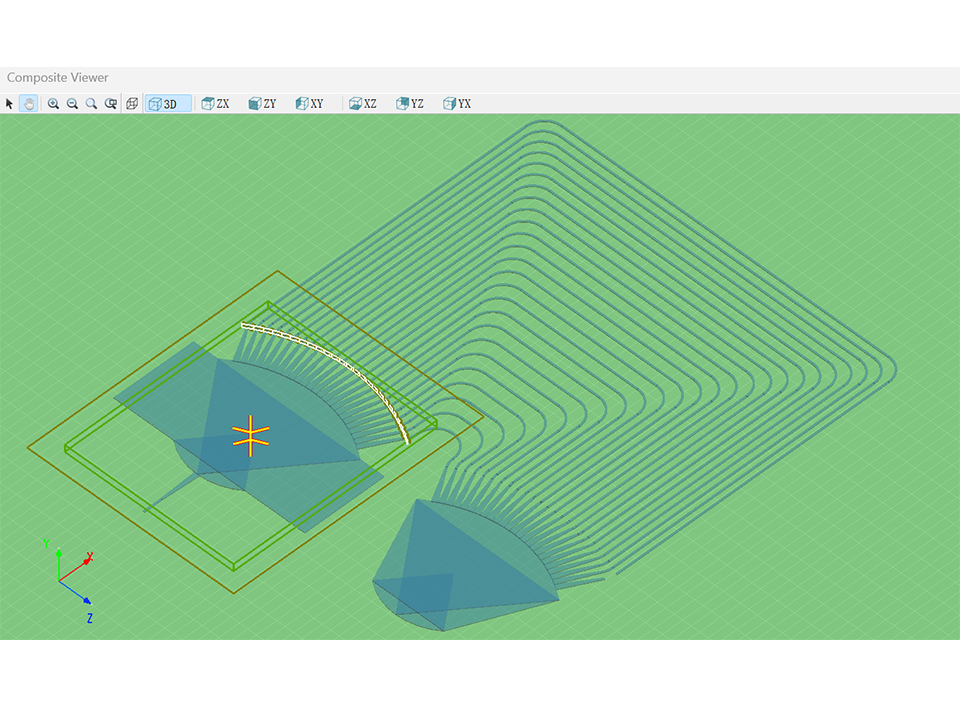
3D CAD界面和丰富的零件库
网格技术
边界条件
_20240115173008A019.png)
多种光源

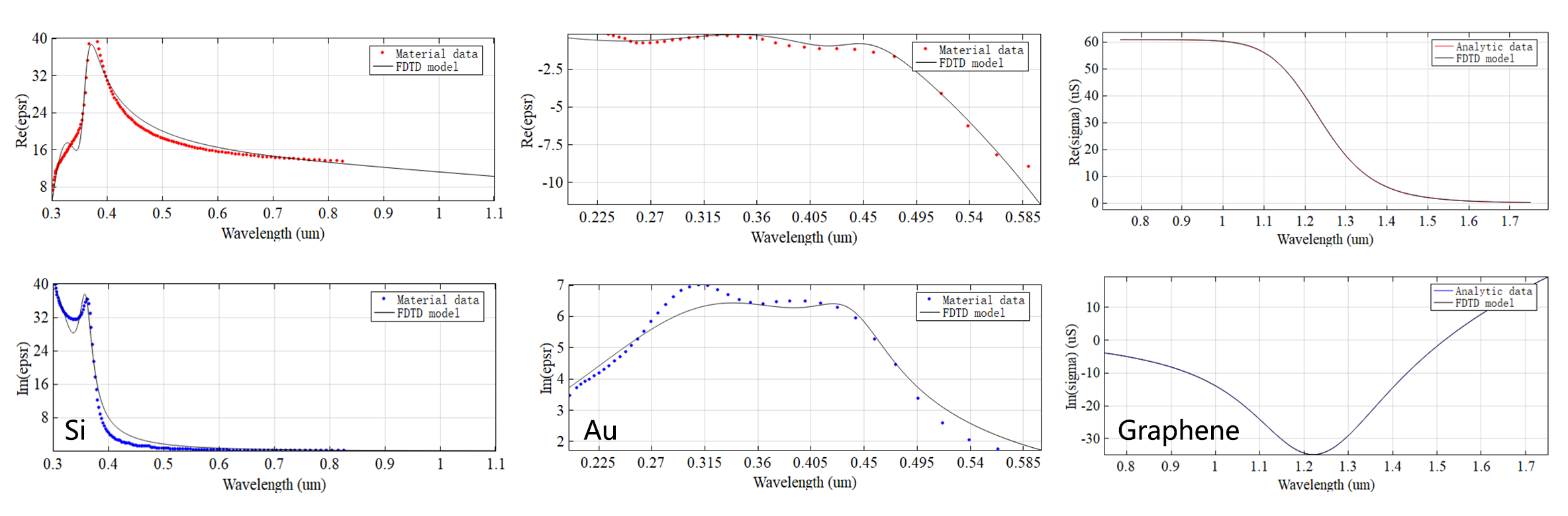
材料属性
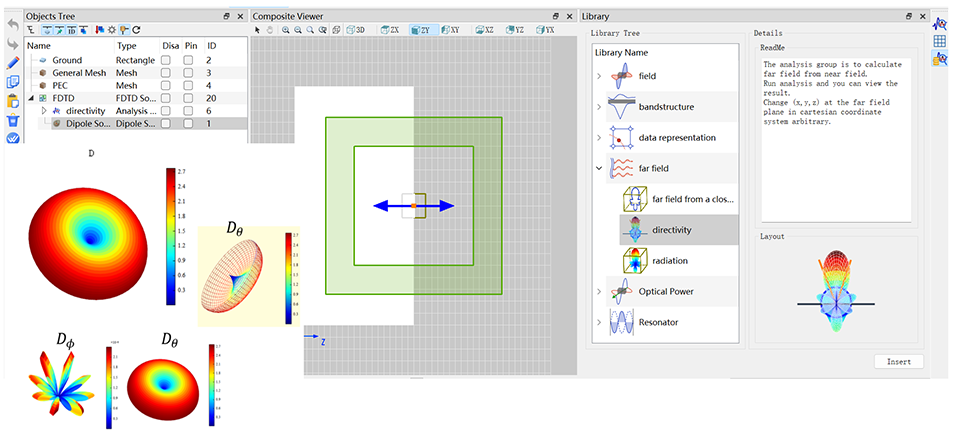
后处理分析
扫描优化
_20240115173926A023.png)
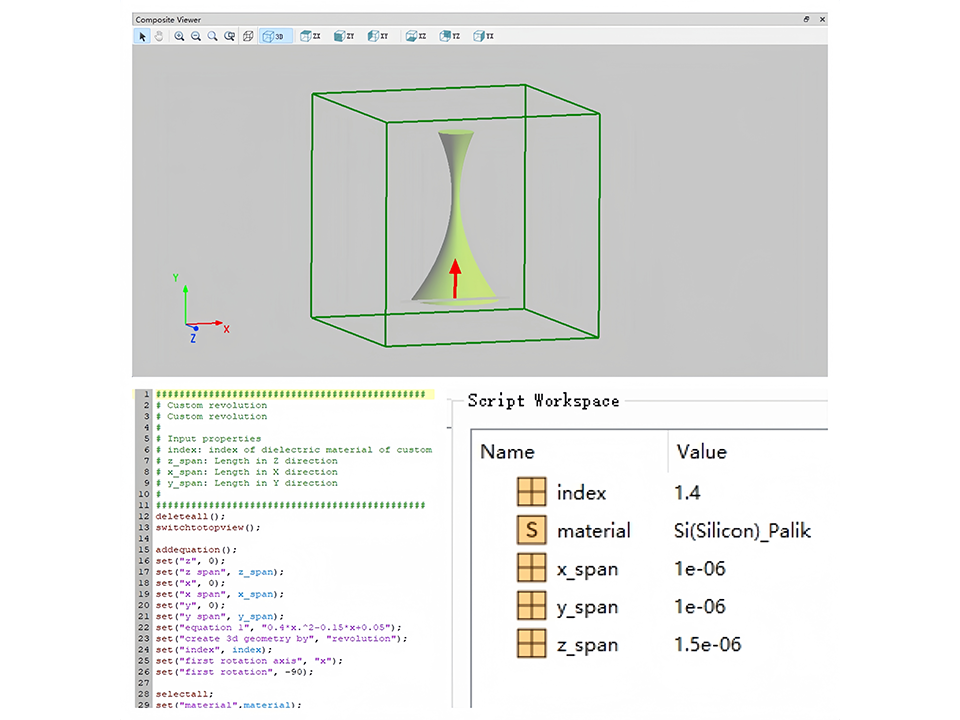
脚本控制
强大的算力

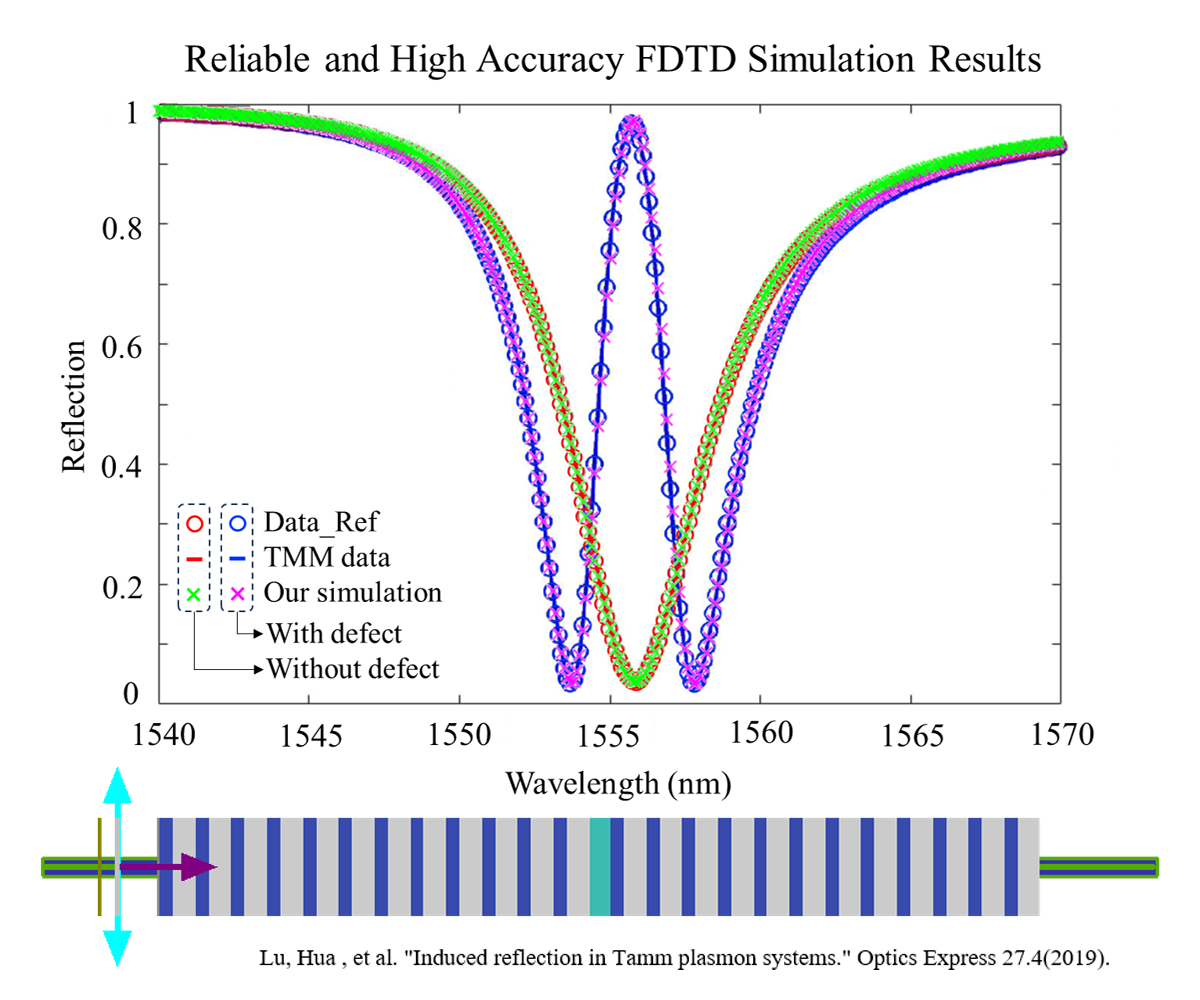
领先行业的超高计算精度
当用户选定要使用的求解器后,仿真任意一个工程简单直接,方便新手快速入门。仿真的主要流程包括如下图展示的步骤。仿真完成后,结果数据可以直接画图展示或者导出到其它关联软件做进一步的分析。
flowchart TB
StructureLibrary( 结构库 )
Material( 材料库 )
SettingTimeSpatial( 设置时空参数 )
SettingMesh( 设置网格 )
SettingBoundary( 设置边界 )
Source(配置光源)
Monitor(配置监视器)
Run(运行仿真)
End[/仿真结束\]
DataVisualizer[(结果可视化)]
isSweep{参数扫描优化?}
Sweep[[扫描优化]]
isPostProcess{后处理分析?}
PostProcess[[后处理分析]]
subgraph obj_sub [配置对象]
direction TB
StructureLibrary
Material
end
subgraph sim_sub [配置求解器]
direction TB
SettingTimeSpatial
SettingMesh
SettingBoundary
end
subgraph sm_sub [光源和监视器]
direction TB
Source
Monitor
end
subgraph FDTDSolver[时域有限差分求解器]
direction TB
Run
End
end
subgraph post_sub[后处理]
isSweep --是--> Sweep
isPostProcess --是--> PostProcess
end
sim_sub --> obj_sub
obj_sub --> sm_sub
sm_sub --> FDTDSolver
Run --> End
FDTDSolver --> DataVisualizer
FDTDSolver --> isSweep
FDTDSolver --> isPostProcess
PostProcess --> DataVisualizer
Sweep -->DataVisualizer
[1] Allen Taflove, "Computational Electromagnetics: The Finite-Difference Time-Domain Method", Boston:Artech House, (2005).
[2] John B. Schneider, "Understanding the Finite-Difference Time-Domain Method", www.eecs.wsu.edu/~schneidj/ufdtd, (2010).