产品
求解器
学习中心
应用案例
知识库
支持
许可协议
发行说明
最新进展
English
中文
客户下载
应用案例
知识库
联系电话
+86-13776637985
邮箱
info@simworks.net


SimWorks FDE 是研究人员和工程技术人员解决大型集成平面光波导、长距离传输器件和各类新型光纤问题的有力工具。下面,我们会简要介绍FDE求解器的基本原理和主要特色。
本征模有限差分求解器(FDE)通过在波导类结构截面网格上求解麦克斯韦方程组来计算模式的空间模场分布和频率特性。FDE的基本原理如下:
通过调整频域麦克斯韦旋度方程系数,可将其简化为如下形式:
根据波导中模的基本形式,电磁场可以写作,,代入麦克斯韦旋度方程后得到电磁场分量表达式。如z轴向磁场分量:
在空间内沿坐标轴线性展开,可将上述方程转换为矩阵形式:
电磁场分量的六个矩阵方程可被转换为求解本征值的问题:
矩阵为差分算法的系数矩阵,向量为需要求解的电磁场分量,为传播常数。
在波导结构截面上生成2DYee cell网格后,材料参数、电场和磁场信息均能被体现在每个网格点。本算法使用稀疏矩阵技术进行矩阵本征值求解,可以得到对应于波导结构的模式分布和有效折射率。
模式数据
FDE求解器类型为2D Y normal时的仿真结果,如下所示。
等效折射率
模式的等效折射率(Effective Index)计算如下:
其中是角频率,是模式的传播常数, 是真空中的光速,是模式的群速度,是自由空间的波矢量。
TE/TM占比
TE/TM占比(TE/TM fraction(%))表示模式中TE和TM模式能量分布相对大小。其计算公式为:
其中为沿传播方向的电场分量,为沿传播方向的磁场分量,为光波导模式截面上的积分面积。
模式损耗
模式的传输损耗(Loss(dB/cm))被计算为:
其中是复折射率的虚部。
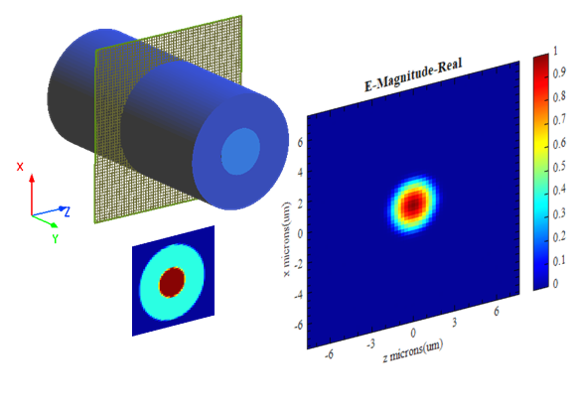
模式耦合被用来计算一个波导中某一输入模式与另一个波导中所有模式之间的场重叠和耦合效率。本软件提供的模式耦合算法基本原理如下。
对于某界面输入场、和输出场、,输入和输出功率分别为:
由于波导中任何场都可以看作是由一系列正交模组成的基组成,所以在反射场可以忽略不记的情况下,输入场和输出场可表示为:
其中系数 、由下式进行计算:
由此可以计算出传输输出场的总功率:
第i个模的模式耦合系数()被计算为:
根据模式耦合的结果得知给定的输入场中,第i个模式的场可以携带多少能量。需要注意的是,本算法是基于理想情况进行计算的,对于传输过程中存在反射或者存在损耗的波导时,计算结果可能并不准确。详细介绍请见Snyder和Love的《光波导理论》。
3D CAD界面和丰富的零件库
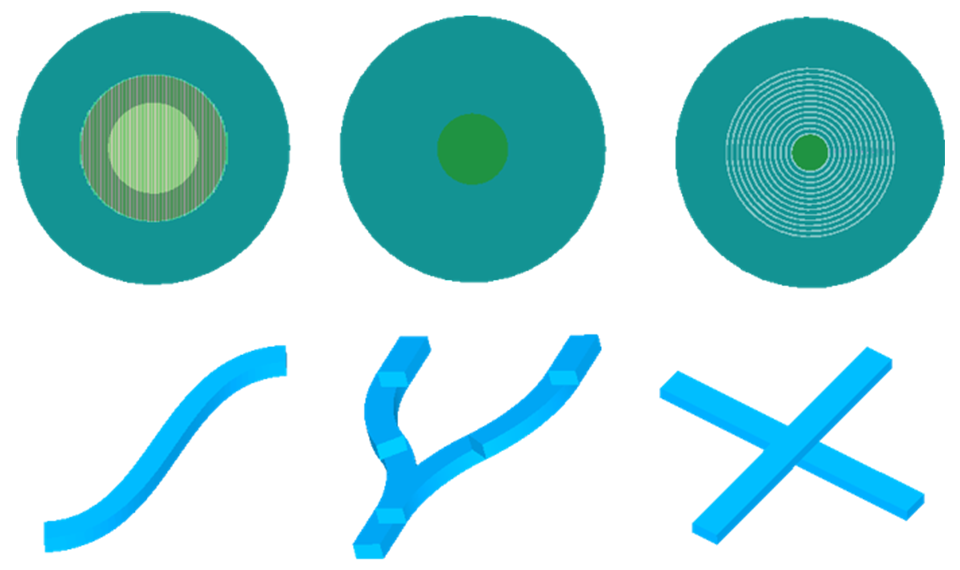
网格技术

边界条件
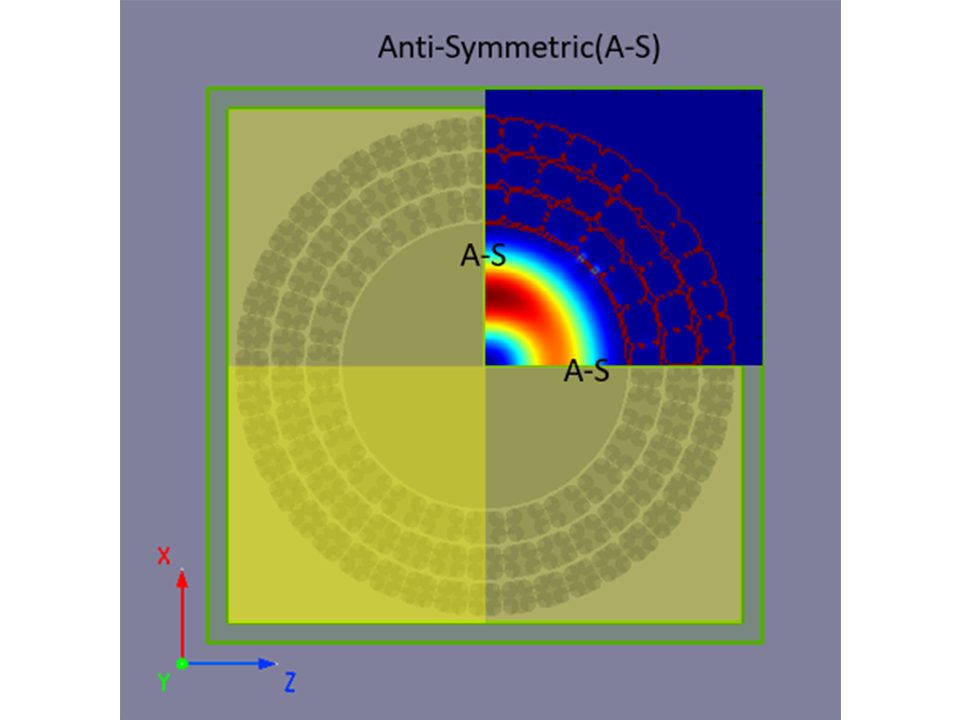
频率分析
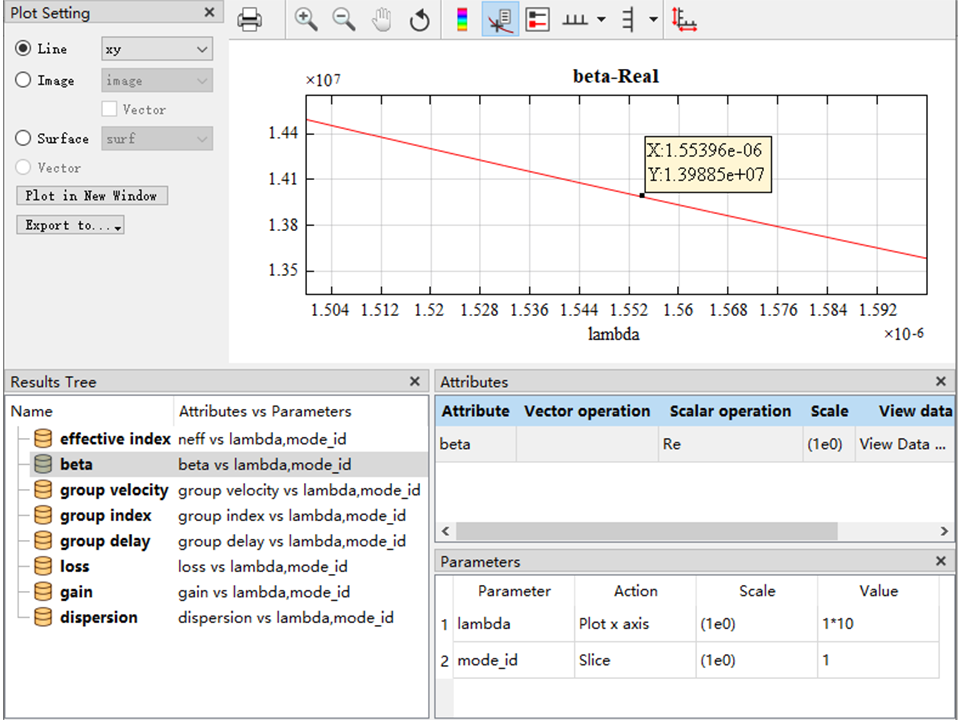
脚本控制
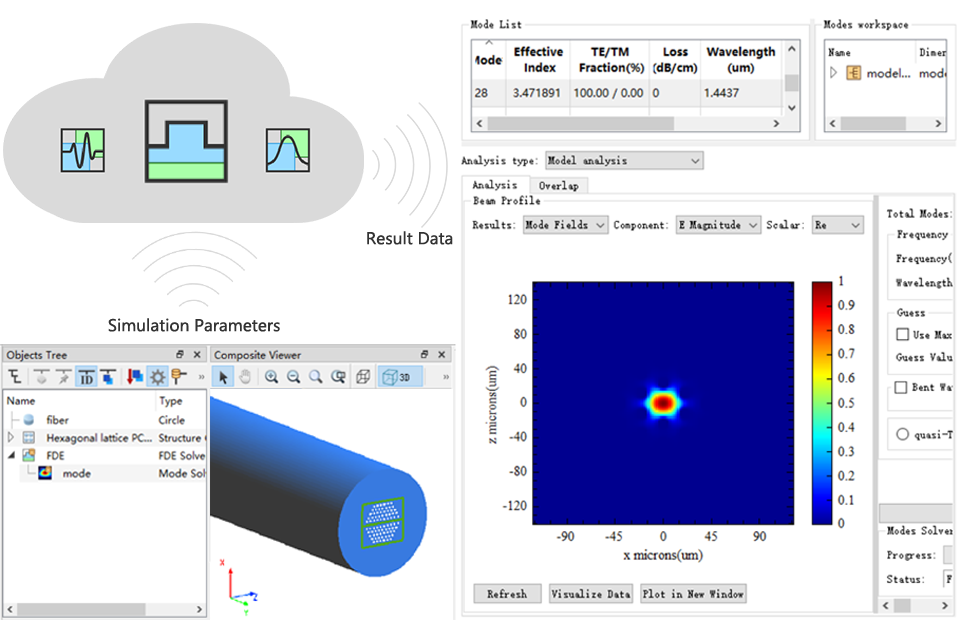
强大的算力
领先行业的超高计算精度
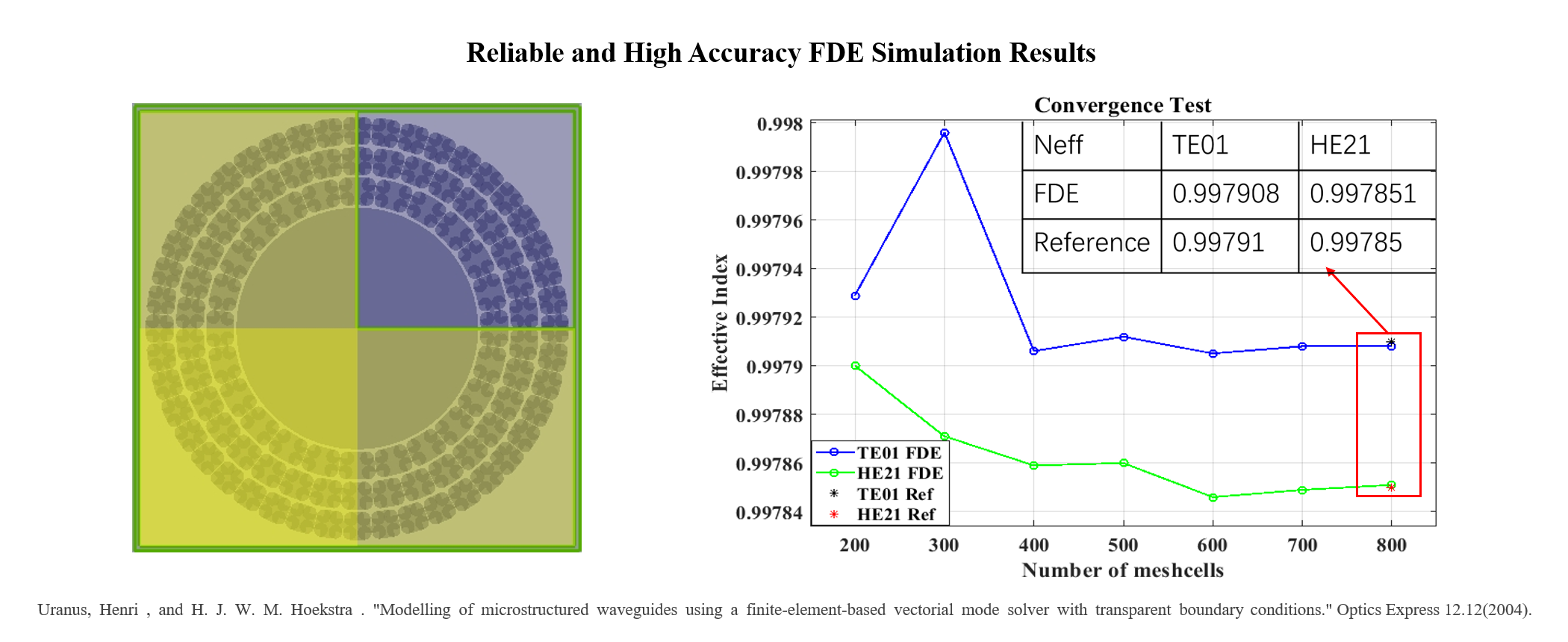
[1]Zhaoming Zhu and Thomas G. Brown, "Full-vectorial finite-difference analysis of microstructured optical fibers," Opt. Express 10, 853-864 (2002)